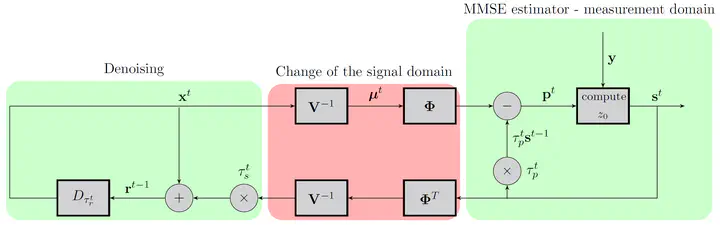
In order to accelerate the reconstruction, it is necessary to either design faster CT operators or develop iterative algorithms that can converge in fewer iterations. In this project, we investigate the use of an emerging reconstruction method from Compressed Sensing (CS), called Approximate Message Passing (AMP), for sparse view CT reconstruction.
AMP based inference refers to a family of iterative algorithms for Compressed Sensing problems with an i.i.d. random Gaussian system matrix and a sparse signal model. AMP is a form of approximate Bayesian inference based on the notion of message passing or loopy belief propagation and is also strongly connected to the family of Expectation Propagation and Expectation Consistent approximation algorithms.
In essence, message passing algorithms work by iteratively updating marginal probabilities on the unknown variables until a locally consistent posterior probability model is obtained. The compelling aspect of the AMP family of algorithms is that they are designed to work in the large system limit (for random systems) which enables the central limit theorem to be invoked. This in turn simplifies the messages to be Gaussian distributions, requiring the algorithm to only pass means and variances. The result is a very efficient algorithm that is remarkably similar to the more traditional iterative shrinkage algorithm but with an additional Onsager correction term. It also has many similarities to the Alternating Direction Method of Multipliers (ADMM) algorithm.